Riddler State Superstrings
Sep 13, 2019
Introduction
The fivethirtyeight riddler this week asks us to make connections between states. Specifically, we want to map the connections between state abbreviations (e.g. CA for California). We've been tasked with finding the longest string of connections where the last letter from one state is the first letter from another, without repeating any states. With 59 state abbreviations to choose from, what is the longest string we can create?
The challenge is to find the longest string of letters in which (1) every pair of consecutive letters is a two-letter state or territory abbreviation, and (2) no state abbreviation occurs more than once. For example, Guam, Utah and Texas can be combined into the valid four-letter string GUTX. Another valid string is ALAK (Alabama, Louisiana and Alaska), while ALAL (Alabama, Louisiana and Alabama) is invalid because it includes the same state, Alabama, twice.
Solution
FMNVIDCALAKSCOHINCTNMPWVARIASDE
This string of nonsense represents the longest possible path between state abbreviations, with 30 connections starting from the Federated States of Micronesia (FM) and ending in Delaware (DE), without any repeats. (As a side note, the longest path between any pair of states starts with FM and ends with DE, but there are 9,984 paths from FM to DE with length 30. I chose this one arbitrarily.) Here's how I calculated it.
In the spirit of several prior problems, I elected to tackle this problem with a graph. The graph formalizes links between states. For example, California (CA) is linked to Alabama (AL), Alaska (AK), American Samoa (AS), Arizona (AZ), and Arkansas (AR) by the letter "A". On the other hand, certain states like Kentucky (KY) are lonelier. No state code begins with the letter Y, so Kentucky doesn't connect outward to any other state. (Don't worry, Alaska (AK) and Oklahoma (OK) connect inwards to Kentucky, so it's not totally alone.)
Between the 59 states there are 168 connections, which we represent in a graph that looks something like this.
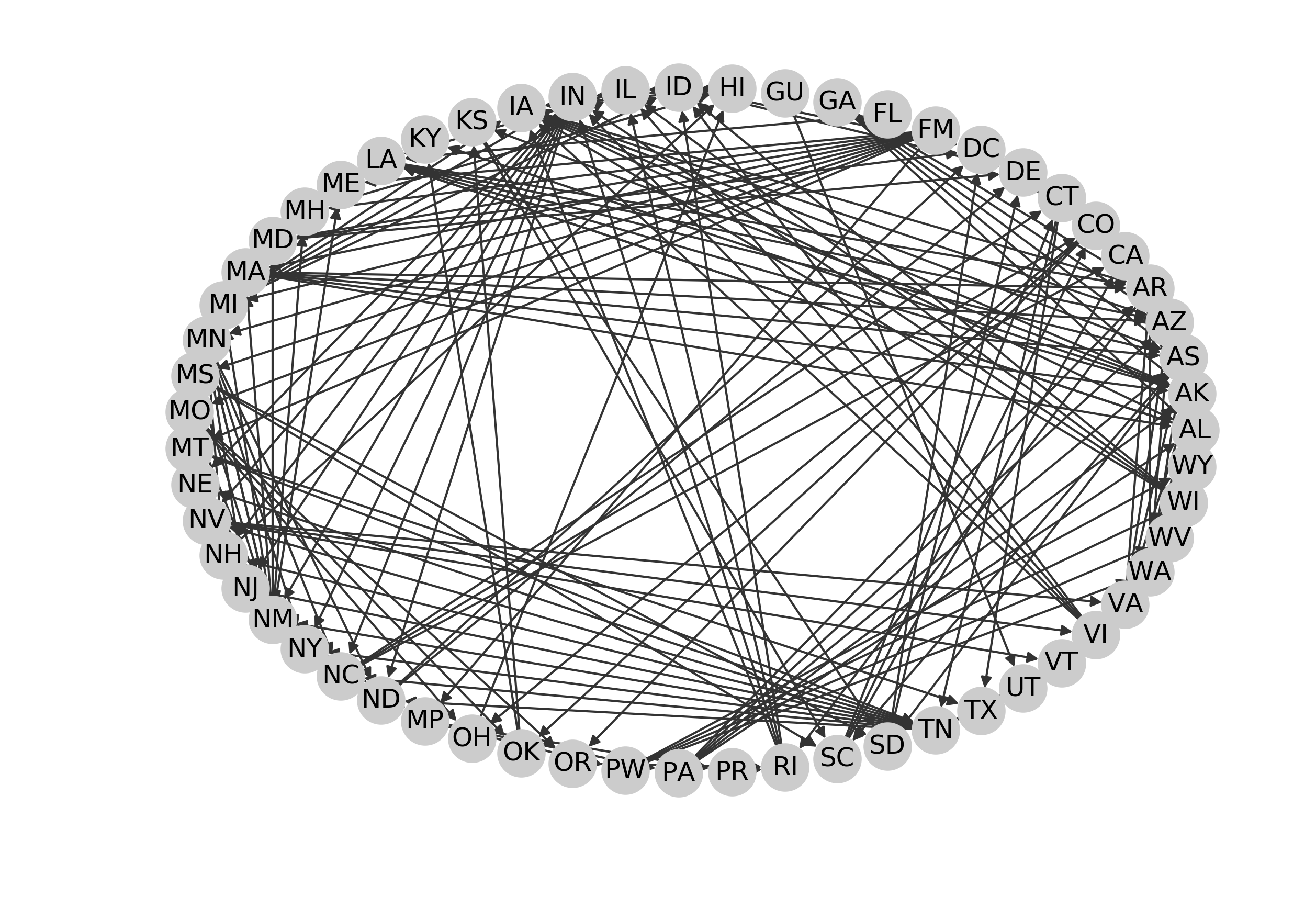
As it turns out, computing the longest path from any starting node to any other node is not an easy problem. It is especially difficult because this graph is cyclical, meaning that you can find yourself in loops of repeating patterns if you're not careful. For example, a loop occurs between CA -> AS -> SC -> CA. Obviously we don't want loops in our result because we're not allowed to repeat states. Therefore, we want simple paths through the graph: paths that visit a node at most one time.
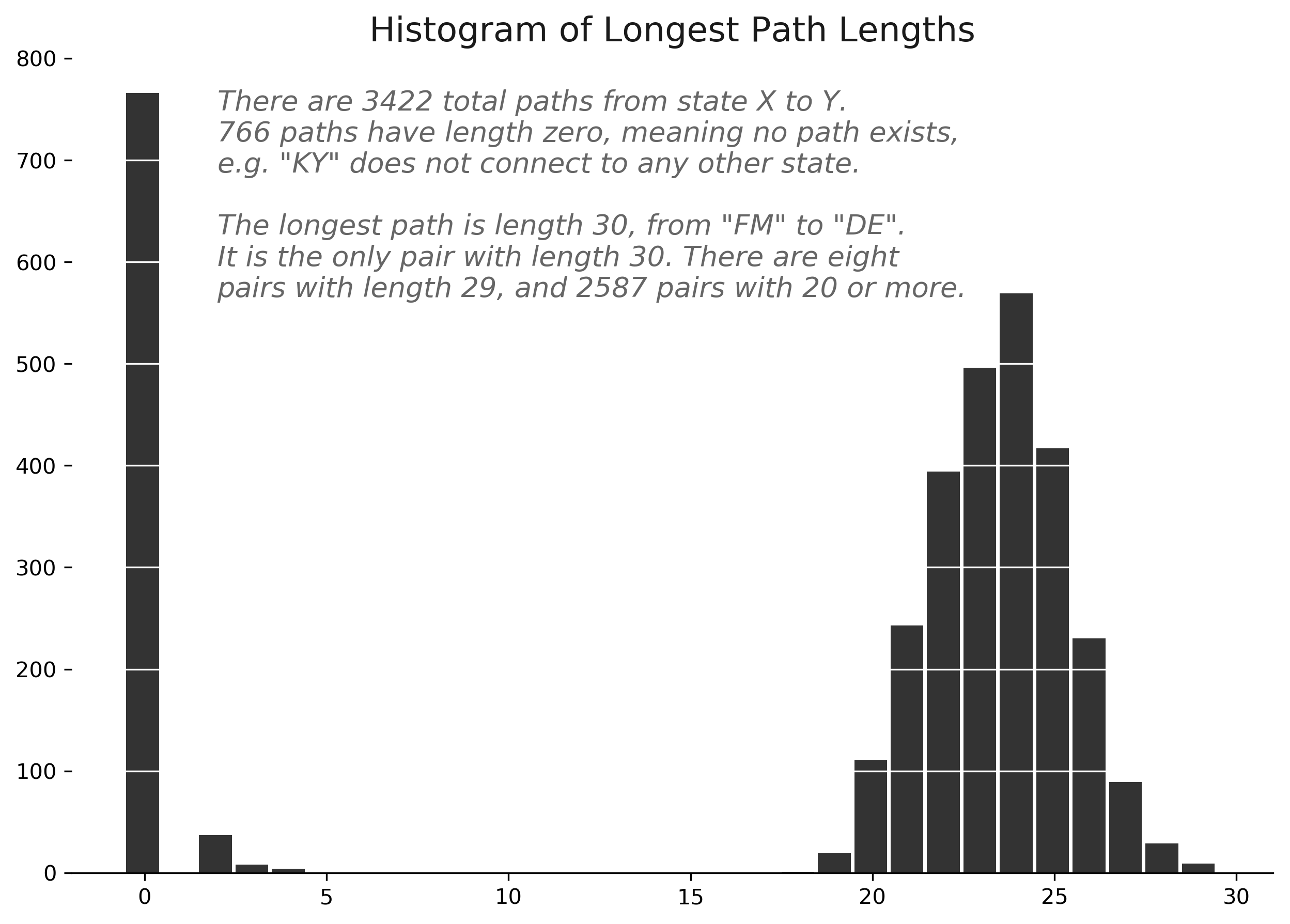
Fortunately, algorithms exist to calculate simple paths through cyclical graphs, but they can be very slow. Despite this, with a bit of patience (82 minutes of patience, to be specific in this case), we can calculate every path between every starting and ending state in the graph. There are total pairs of states, and we measure the longest path between each pair. Then we just need to select the longest one from all the pairs.
As it turns out, most paths tend to include at least 20 states, as shown by the chart below. On the other hand, several starting-ending state pairs have no connections, such as Kentucky, that can't connect outward to any other state. The chart below shows a histogram of all the longest paths between each pair of states.
Full Code
The full code this week is fairly straightforward to read, but takes quite a while to calculate. The model function took well over an hour to run on my computer. Fortunately, I saved the full results if you want to skip the calculation and look at the raw output. Each state pair is represented here, with one example of the longest simple path you could take between the two.
import json
import networkx as nx
from itertools import permutations
from tqdm import tqdm
STATES = {
'Alabama': 'AL',
'Alaska': 'AK',
'American Samoa': 'AS',
'Arizona': 'AZ',
'Arkansas': 'AR',
'California': 'CA',
'Colorado': 'CO',
'Connecticut': 'CT',
'Delaware': 'DE',
'District of Columbia': 'DC',
'Federated States of Micronesia': 'FM',
'Florida': 'FL',
'Georgia': 'GA',
'Guam': 'GU',
'Hawaii': 'HI',
'Idaho': 'ID',
'Illinois': 'IL',
'Indiana': 'IN',
'Iowa': 'IA',
'Kansas': 'KS',
'Kentucky': 'KY',
'Louisiana': 'LA',
'Maine': 'ME',
'Marshall Islands': 'MH',
'Maryland': 'MD',
'Massachusetts': 'MA',
'Michigan': 'MI',
'Minnesota': 'MN',
'Mississippi': 'MS',
'Missouri': 'MO',
'Montana': 'MT',
'Nebraska': 'NE',
'Nevada': 'NV',
'New Hampshire': 'NH',
'New Jersey': 'NJ',
'New Mexico': 'NM',
'New York': 'NY',
'North Carolina': 'NC',
'North Dakota': 'ND',
'Northern Mariana Islands': 'MP',
'Ohio': 'OH',
'Oklahoma': 'OK',
'Oregon': 'OR',
'Palau': 'PW',
'Pennsylvania': 'PA',
'Puerto Rico': 'PR',
'Rhode Island': 'RI',
'South Carolina': 'SC',
'South Dakota': 'SD',
'Tennessee': 'TN',
'Texas': 'TX',
'Utah': 'UT',
'Vermont': 'VT',
'Virgin Islands': 'VI',
'Virginia': 'VA',
'Washington': 'WA',
'West Virginia': 'WV',
'Wisconsin': 'WI',
'Wyoming': 'WY',
}
def paths(state_codes):
"""
Returns a list of tuples of state codes, where the
last letter of the first state code matches the
first letter of the last state code, e.g.
('WA', 'AL'), or ('DC, 'CA')
Parameters
----------
state_codes : iterable of codes, e.g. ['AL', 'AK', 'AS', ...]
Returns
-------
paths : list of tuples, e.g. [('WA', 'AL'), ('DC, 'CA'), ...]
"""
return [
x for x in permutations(state_codes, 2)
if x[0][1] == x[1][0]
]
def graph(state_codes):
"""
Returns the directed graph of linked state codes
Preserves the order of state_code when building the graph
"""
G = nx.DiGraph()
G.add_nodes_from(state_codes)
G.add_edges_from(paths(state_codes))
return G
def longest_simple_path(graph, source, target, **kwargs):
"""Finds the longest simple path between two nodes in a graph"""
paths = nx.all_simple_paths(G=graph, source=source, target=target, **kwargs)
try:
return max(paths, key=len)
except ValueError:
# paths is an empty sequence
return []
def model(state_codes):
"""
Returns a dictionary with tuple keys and list values, e.g.
[('FM', 'DE')] = ['FM', 'MN', 'NV', 'VI', 'ID', ... , 'DE']
This is an exhaustive search of the longest simple paths between
all possible states in the state_codes list, so is guaranteed to
find the longest possible path between any two codes.
WARNING : this function took 82 minutes to run on my computer
for all 3422 paths. Uses tqdm to display a progress bar
"""
out = {}
G = graph(state_codes)
for s, t in tqdm(list(permutations(state_codes, 2))):
out[(s, t)] = longest_simple_path(G, source=s, target=t)
return out
def write_json(state_codes, file_name):
"""Outputs the results of the model to a json file"""
# replace tuple keys ('X', 'Y') with "X-Y" as a string
results = {f'{k[0]}-{k[1]}': v for k, v in model(state_codes).items()}
with open(file_name, 'w') as file:
file.write(json.dumps(results), indent=4)
return None