Introduction

We are carefully coloring a poster in this week's Riddler. We want to draw horizontal lines with a marker in order to fill the poster with ink as evenly as possible. How far apart should each marker line be? We'll use numpy for a computational approach that minimizes the standard deviation of our coloring scheme.

Some friends have invited you to a protest, and you’ll be making a sign with large lettering. You’re filling in the sign’s letters by drawing horizontal lines with a marker. The marker has a flat circular tip with a radius of 1 centimeter, and you’re holding the marker so that it’s upright, perpendicular to the sign.

Since the diameter of the marker’s tip is 2 centimeters, you decide to fill in the letters by drawing lines every 2 centimeters. However, this is the pattern you get:

The shading doesn’t look very uniform — each stroke is indeed 2 centimeters wide, but there appear to be gaps between the strokes. Of course, if you drew many, many lines all bunched together, you’d have a rather uniform shading.

But you don’t have all day to make this sign. If the lines can’t overlap by more than 1 centimeter — half the diameter of the marker tip — what should this overlap be, in order to achieve a shading that’s as uniform as possible? And how uniform will this shading be, say, as measured by the standard deviation in relative ink on the sign?

Solution

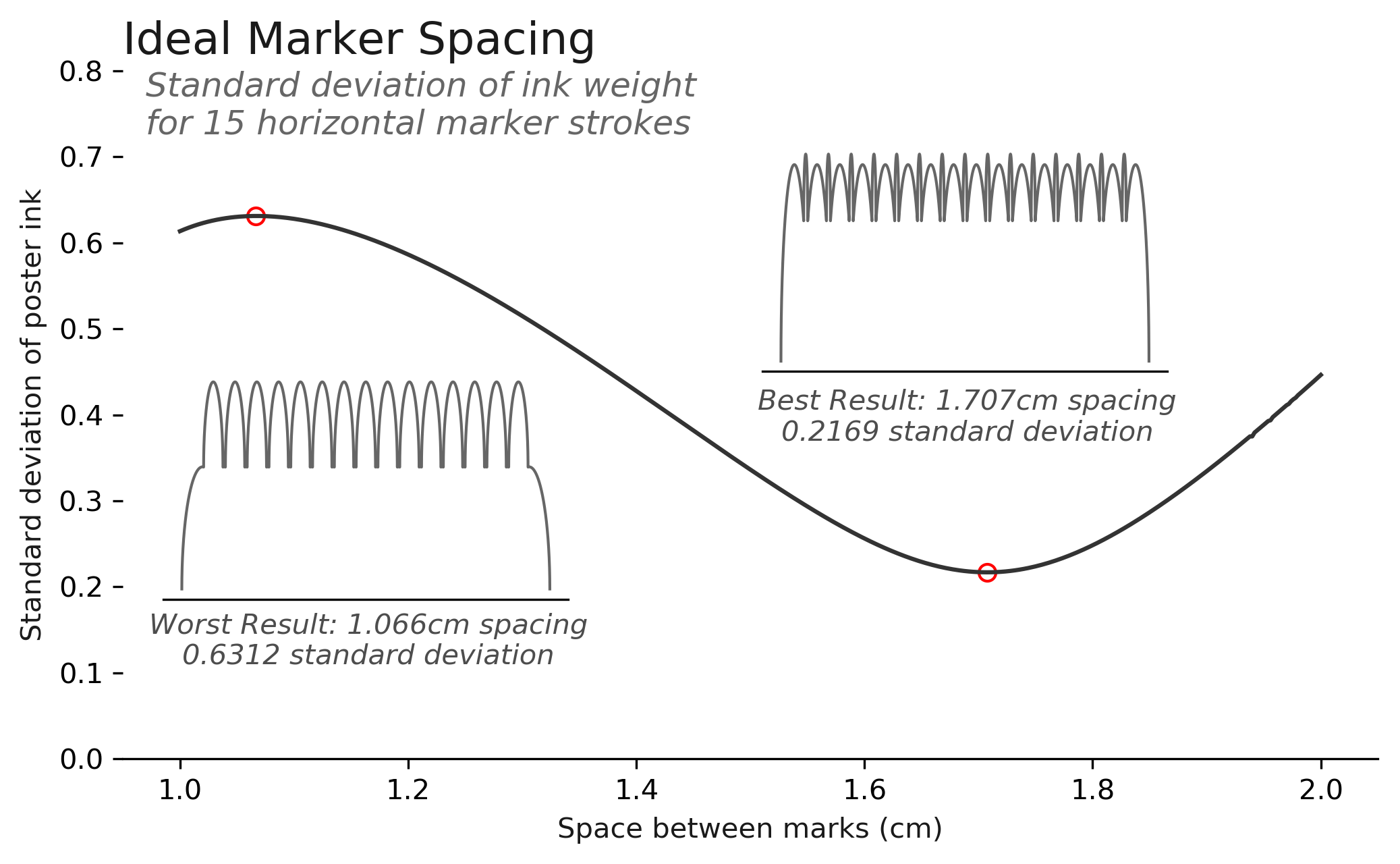
The ideal spacing between marker strokes is roughly 1.7cm. Assuming you could be that precise, the standard deviation of ink should be roughly 0.217. I made the following assumptions in order to calculate this result.

1. The top and bottom strokes are set 1cm away from the edge so you're still coloring within the lines. Each stroke between those will be spaced $x$ centimeters apart, where we try to solve for the value of $x$ that minimizes the overall standard deviation.
2. Somewhat arbitrarily, I've chosen 15 marker strokes between the top and bottom. This affects the standard deviation value I calculated, but shouldn't affect the ideal spacing.
3. I assumed ink is perfectly additive: if you color a section of the poster twice, the total ink on that spot is the sum of ink from both marker strokes with no loss.
4. The amount of ink deposited by a marker stroke is equal to the cross sectional area of the marker tip, which is a circle.
5. The standard deviation of a particular spacing is equal to the standard deviation of marker ink along a vertical slice of the poster.

The chart below illustrates how the standard deviation changes as a function of the marker spacing. The dark wavy line in the middle represents the standard deviation for a given spacing on the x-axis. This line is minimized when spacing is 1.7cm, and is maximized at 1.07cm. The insets in the chart show a vertical cross section of ink for a slice of the poster. Standard deviation at each point is calculated based on the values in the inset charts. We can see that the values of the upper right inset chart are more consistent overall, which is reflected in the lower standard deviation. The other inset chart has more variance in the ink values, so its standard deviation is higher.

Full Code

I took a purely computer-based approach to solve this week's problem. While it's probably possible to write the equation for the lines in my chart above, it gets complicated quickly. Instead, I used numpy to simulate one million points across a vertical slice of the poster and tally the ink at each point on the slice.

I assumed the marker leaves ink on the poster in proportion to the slice of marker tip at each point. So the cross_section function is essentially the equation for a circle. The ink_weight function returns the array for the inset charts above, which is the basis for calculating the standard deviations. I added a quick plotting method called plot_ink as well to visualize any given spacing.

Finally, I used a list comprehension to calculate the standard deviation for 500 different spacing values from 1.0 to 2.0, and found the minimum at roughly 1.7cm.

from typing import Optional
from matplotlib import pyplot as plt
import numpy as np


def cross_section(
   x: np.ndarray,
   center: np.ndarray,
   radius: float = 1.0
) -> np.ndarray:
    """
    Returns the length of the cross section of a circle at a position, x,
    centered at a given point with a given radius. If x == center, then this
    returns the diameter of the circle. If x == center + radius, then this
    returns zero.

    Examples
    --------
    >>> cross_section(x=np.array([1.0]), center=np.array([1.0]))
    array([[2.]])

    >>> cross_section(x=np.array([0.0]), center=np.array([1.0]))
    array([[0.]])
    """
    return 2 * np.maximum(0, (1 - (x - center[:, None]) ** 2)) ** 0.5


def ink_weight(
    spacing: float,
    strokes: int,
    radius: float = 1.0,
    points: int = 1000000,
) -> np.ndarray:
    """
    Returns an array of values with shape (points,) that represents the total
    ink weight of that slice of the poster. It's essentially a vertical slice
    of the ink on the poster from top to bottom, which sums the amount of ink
    from each marker stroke.

    Parameters
    ----------
    spacing : float, must be in the range [radius, 2*radius].
    strokes : int, the number of marker strokes used on the poster
    radius : float, default 1.0, the radius of the marker
    points : int, the number of points to measure; more points gives a more
        accurate answer, but may take slightly longer to compute

    Returns
    -------
    x : np.ndarray, an array of the x-coordinates of the ink_weight array
    ink_weight : np.ndarray, an array of total marker weight from each stroke

    Raises
    ------
    ValueError, if the spacing arguments is not within an acceptable range
    """
    # raise an error if spacings are closer than 1cm (not allowed)
    if spacing < radius or spacing > 2 * radius:
        raise ValueError(
            f"Spacing must be between {radius} and {2 * radius}; "
            f" you provided {spacing}."
        )

    x = np.linspace(0, 2 * radius + spacing * strokes, points)
    centers = np.arange(radius, radius + spacing * (strokes + 1), spacing)
    weights = cross_section(x, centers).sum(0)
    return x, weights


def plot_ink(
    spacing: float,
    strokes: int,
    radius: float = 1.0,
    points: int = 1000000,
    output: Optional[str] = None,
) -> None:
    """
    Plot the slice of ink weight on the poster

    Parameters
    ----------
    spacing : float, must be in the range [radius, 2*radius].
    strokes : int, the number of marker strokes used on the poster
    radius : float, default 1.0, the radius of the marker
    points : int, the number of points to measure; more points gives a more
        accurate answer, but may take slightly longer to compute
    output : Optional[str], default None, if provided, the string name that
        should be used to save the file, e.g. "path/to/plot.png"
    """
    fig, ax = plt.subplots(figsize=(8, 4.5))

    x, weight = ink_weight(spacing, strokes, radius, points)
    ax.plot(x, weight, color="0.2")

    ax.set_ylim(0, weight.max() * 1.05)
    for s in ["top", "right", "left"]:
        ax.spines[s].set_visible(False)
    if output:
        plt.savefig(output, bbox_inches="tight", dpi=300)
    return None


if __name__ == "__main__":
    import doctest

    doctest.testmod()