Riddler Elves
Dec 21, 2018
Introduction
This week's holiday Riddler is a twist on the classic "birthday problem". The birthday problem asks us to calculate the probability that at least two people at a party have the same birthday. Most people hearing this problem for the first time are surprised at how few people you need - roughly 23 people results in 50% odds of finding at least one pair of birthdays! For this problem, we're interested in calculating how likely we are to hear the same song more than once from a shuffled playlist. Moreover, what can we infer about the size of the playlist, given that we hear repeats roughly half the time? Here is the exact problem we'll solve.
In Santa’s workshop, elves make toys during a shift each day. On the overhead radio, Christmas music plays, with a program randomly selecting songs from a large playlist.During any given shift, the elves hear 100 songs. A cranky elf named Cranky has taken to throwing snowballs at everyone if he hears the same song twice. This has happened during about half of the shifts. One day, a mathematically inclined elf named Mathy tires of Cranky’s sodden outbursts. So Mathy decides to use what he knows to figure out how large Santa’s playlist actually is.
Help Mathy out: How large is Santa’s playlist?
The Birthday Problem
The birthday problem is usually described like this: suppose you attend a party with total people, including yourself. What value of gives a 50% chance that at least two people share a birthday?
Often in questions of probability it helps to calculate the odds of the event we're not interested in, and then we find the probability we care about by the property of complementarity. We can do this, because there are only two options: either there are no shared birthdays at all, or there are at least two shared birthdays. Therefore, the probability of one outcome is one minus the probability of the other outcome. As a result, we will calculate the probability that nobody in the room shares a birthday, then subtract that value from one for the answer we really want.
In a group of two people, the probability of distinct birthdays is . In other words, we only need to calculate the probability that the second person has any other birthday than the first person. In a group of three people, we need to check that the third person has a different birthday than the first person and the second person, so we get . We can continue this pattern for any number of people, and we get the following formula for a group of size :
Most people are surprised to learn that a group of 23 people has a 49.3% chance of all unique birthdays, or a 50.7% chance of at least one shared birthday. Fortunately, we can use the same framework to solve the Riddler.
Solution
Now we have a general purpose formula for the odds of picking unique elements from a group of size . In the birthday problem we are given and asked to solve for such that the outcome is 50%. This week's Riddler asks us a related question, where we are given and asked to solve for such that the outcome is 50%. Therefore we want to solve:
Fortunately, we can delegate the computation to Python and quickly solve for any value of .
import numpy as np
def model(songs_heard, playlist_size):
"""
Returns the probability of hearing a repeat song, given
a number of "songs_heard" and a total "playlist_size"
"""
if songs_heard >= playlist_size:
return 1.
else:
s = np.arange(playlist_size - songs_heard + 1, playlist_size + 1) / playlist_size
return 1 - s.prod()
# birthday problem
>>> model(23, 365)
0.5072972343239853
# riddler example
>>> model(100, 7500)
0.48466504008664024
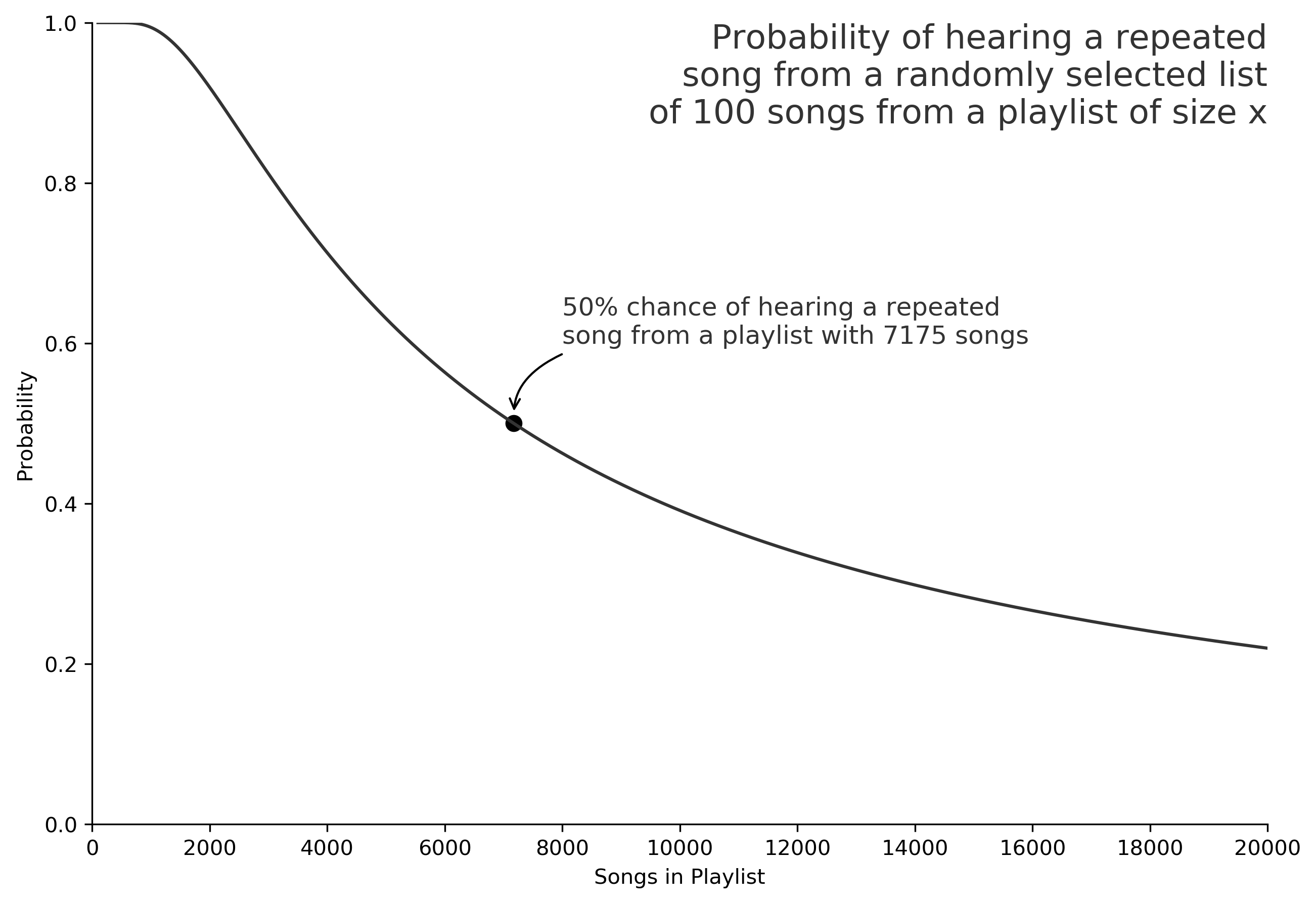
For and , we expect to hear repeated songs 48.5% of the time. Therefore, we know that the actual playlist should have fewer than 7500 songs. (When we lower the number of total songs available, the probability of hearing the same song repeated goes up.) After a few trials, we find the following:
>>> model(100, 7175)
0.4999798251579207
>>> python(100, 7174)
0.5000283570392747
If the playlist has 7175 songs in it and we listen to 100 randomly chosen songs, we'd expect to hear repeats 50% of the time. It's unclear if Cranky is accurate in his measurements out to the hundred-thousandths place, but the playlist with 7175 songs is the closest value to 50%, so that seems reasonable. Therefore, we conclude that Santa's playlist has 7175 songs in it.
The chart below plots the expected probability of hearing a repeat for various playlist sizes.