Riddler Bacteria
Jun 12, 2020
Introduction
We're studying simulated petri dishes in this week's Riddler! We want to figure out how likely a colony of bacteria is to survive, given what we know about how often its cells divide. This is a classic problem that can be modeled with a stochastic process, but we'll try a different approach with very large markov transition matrices built in python and numpy.
You are studying a new strain of bacteria, Riddlerium classicum (or R. classicum, as the researchers call it). Each R. classicum bacterium will do one of two things: split into two copies of itself or die. There is an 80 percent chance of the former and a 20 percent chance of the latter.If you start with a single R. classicum bacterium, what is the probability that it will lead to an everlasting colony (i.e., the colony will theoretically persist for an infinite amount of time)?
Extra credit: Suppose that, instead of 80 percent, each bacterium divides with probability p. Now what’s the probability that a single bacterium will lead to an everlasting colony?
Solution
With its 80% doubling rate, the R. classicum bacteria has a 75% chance to survive indefinitely. (It's unclear if its sibling bacteria, Riddler Expressum, would be so resilient...)
The survival rate is highly dependent on the doubling rate, as the chart below shows. For doubling rates less than 50%, a colony of bacteria will surely go extinct, but for doubling rates above 50%, the survival odds improve substantially.
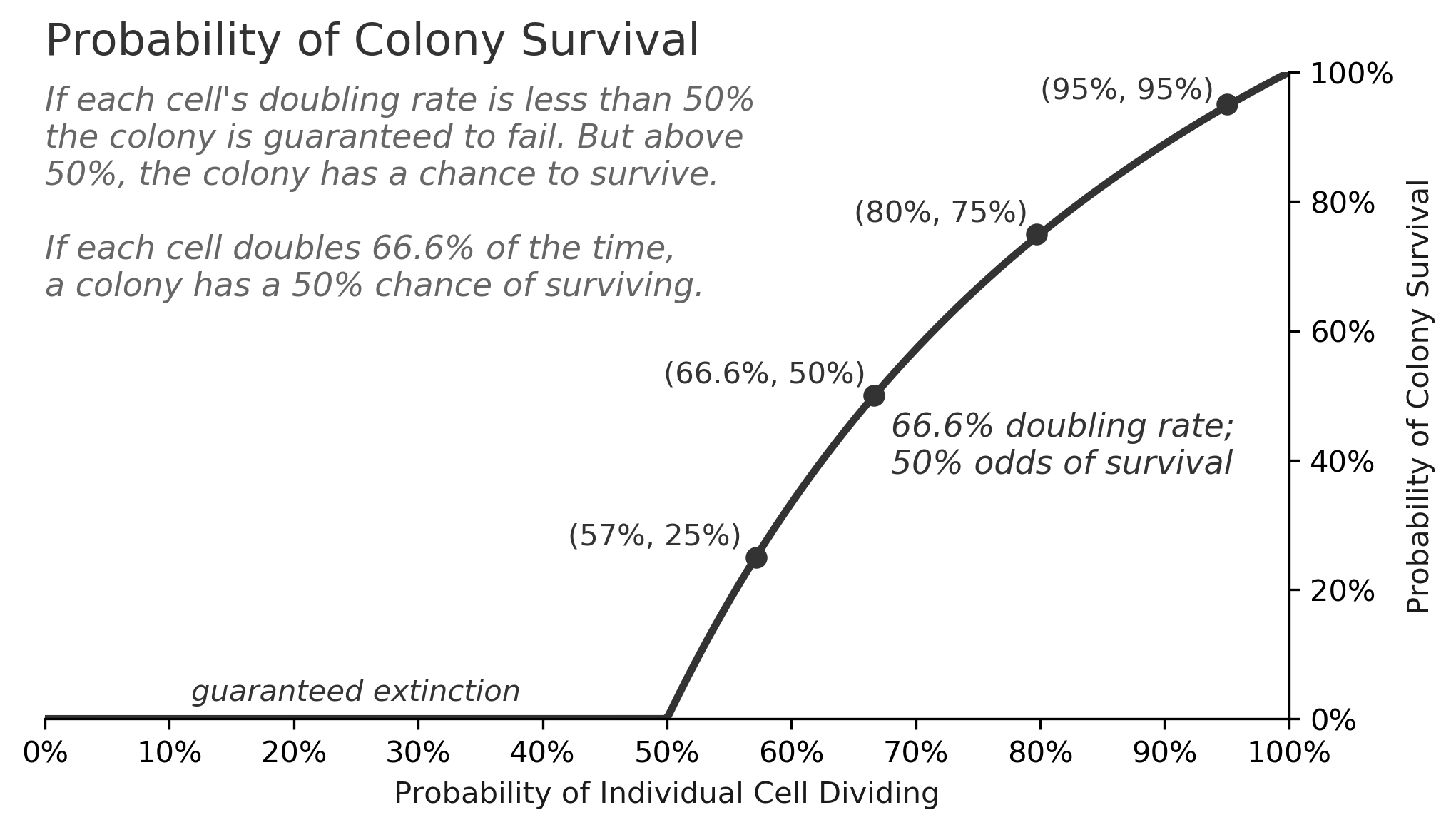
This class of problem, called a "birth-death process", can get very complicated, but for this simple case of cells doubling or dying, there is a formula for the survival rate as a function of :
This tells us that the survival rate for a colony with an 80% doubling rate is , or 75%. It also tells us that it's impossible for a colony of bacteria to survive if the doubling rate is less than 50%.
Methodology
Birth-death problems can get pretty gnarly, but this particular version is one of the simpler cases: a cell may only divide or die, and cells can't leave or enter the closed system. In continuous time, the colony can be modeled using a stochastic process, which is a mathematical model that lets us simulate the behavior of systems which behave randomly over time.
Small plug: I've actually been working on an open source python library to model stochastic processes in the financial markets, called
pyesg. This library lets you simulate random processes like stocks, interest rates, or energy prices, which you could use to simulate investment portfolios, decide which mortgage to choose, or plan for market downturns. Check it out on github!
There's also another way to model this process. We can model time in discrete steps, simulating whether each cell in the colony divides or dies, and track the population size over time. For example, a starting population of 6 could become a population of , based on which cells divide or die. The odds of each new population are called transition probabilities. We want to create a matrix of these transition probabilities to be able to determine the long term behavior of the system, which is a technique I've used on many prior Riddler puzzles.
The difference here is that the colony population can theoretically grow to infinite size, and the typical markov chain transition matrix approach only works for finite-sized matrices. While it might seem like this is a dead end, we can work around it.
We are interested in three possible states: permanent colony extinction (☠), indefinite colony survival, or a transient state between the two. Rather than trying to model an infinite population, we'll assume that a sufficiently large population, e.g. 500 or 1000 cells, eventually leads to survival. In other words, with a large enough finite matrix, our answer should approach the true answer.
In my experiments, a matrix with size 500 seemed to converge nicely to the true result, and was quick to compute. Ultimately, the survival_probability function tells us how likely it is for a colony to reach a given size before going extinct. For example, here's the calculation for the original problem, with the 80% doubling rate.
survival_probability(n=500, p=0.8)
# 0.7500000000000211
Full Code
This week's code is almost entirely linear-algebra-as-code. There's a function that generates a markov transition matrix of any size, and a function that uses the transition matrix to calculate the expected probability that the colony survives indefinitely.
My chart was made by calling the survival_probability function in a list comprehension to evaluate the survival probabilities at many values between 0 and 1.0.
from typing import Dict
import numpy as np
from scipy.stats import binom
def transition_matrix(n: int, p: float = 0.8) -> np.ndarray:
"""
Generates a transition matrix for a maximum population of size n, where
the population can take even number values from 0 to n or ∞. The matrix
will have size (n // 2 + 3, n // 2 + 3), where each row represents the
transition probability from state X to state Y, and the absorbing states
are either 0 (extinction) or ∞ (everlasting survival). As n -> ∞, we can
create better estimates of the true rate of everlasting survival.
The matrix is ordered by: [1, n, n - 2, n - 4, ..., 0, ∞], where each
value represents a possible population size, and this particular ordering
(called the canonical form) makes some of the linear algebra easier later
Parameters
----------
n : int, the maximum population size to model
p : float, the probability of dividing into two cells
Returns
-------
M : np.ndarray, the transition matrix with size (n // 2 + 3, n // 2 + 3)
Examples
--------
>>> transition_matrix(n=4)
array([[0. , 0. , 0.8 , 0.2 , 0. ],
[0. , 0.1536, 0.0256, 0.0016, 0.8192],
[0. , 0.64 , 0.32 , 0.04 , 0. ],
[0. , 0. , 0. , 1. , 0. ],
[0. , 0. , 0. , 0. , 1. ]])
"""
# create the transition matrix one row at a time, from n == 2 to n == n
# then stack each of those on top of two absorbing states at 0 and ∞.
# for transitions to values greater than n we group them into the ∞ row.
M = np.zeros(shape=(n // 2 + 3, n // 2 + 3), dtype=np.float64)
idx = np.arange(n + 1)[::-1]
for x in range(1, n // 2 + 1):
pmf = binom(n=x * 2, p=p).pmf(idx)
M[-x - 2, 1:-1] = pmf[-n // 2 - 1:]
M[-x - 2, -1] = pmf[:-n // 2 - 1].sum()
M[:, 0] = 0.0
M[0, :] = 0.0
M[-2:, :] = 0.0
M[[-2, -1], [-2, -1]] = 1.0
M[0, -3] = p
M[0, -2] = 1 - p
return M
def survival_probability(n: int, p: float = 0.8) -> float:
"""
Returns the survival probability for a population with a max size of n,
which represents the probability that a cell colony starting with one
cell will eventually survive or become extinct.
Parameters
----------
n : int, the maximum population size to model
p : float, the probability of dividing into two cells
Returns
-------
result : float, the probability of the colony surviving indefinitely
Examples
--------
>>> survival_probability(n=6)
0.7500074825177829
>>> survival_probability(n=500)
0.7500000000000211
"""
M = transition_matrix(n=n, p=p)
Q = np.linalg.inv(np.eye(len(M) - 2) - M[:-2, :-2])
R = M[:-2, -2:]
return (Q @ R)[0, 1]
if __name__ == "__main__":
import doctest
doctest.testmod()